This post was inspired by a customer who asked us for some help solving a problem. We asked him if it was okay with him if we did a Money Blog post about a situation like his, and he said that would be fine. So here goes!
THE SCENARIO
I came across a note for sale. The terms of the note are as follows:
Original balance: $6,000
Unpaid balance as of June 2: $4,560
Term: 5 years
Interest Rate: 0
Payments: $100 per month
If I buy it, make the purchase on June 2, and the first payment I'll receive will be the July payment.
Every February, the borrower pays off $1,000 in order to accelerate the note paydown.
QUESTION
If the borrower continues to pay on his normal schedule (including the extra $1,000 every February), how much longer will he continue to owe the note's owner anything?
SOLUTION
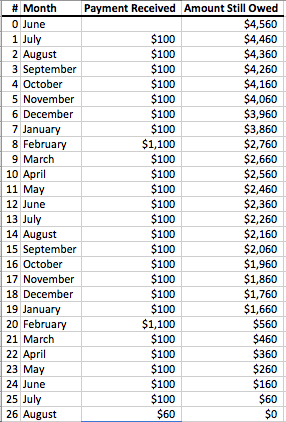
I'll start receiving money in July. That means that I'll receive $100 for each of July through January (6 payments for a total of $600), then $1100 in Febuary, then $100 for each of March through January (11 payments for a total of $1,100), and so on.
So as of next January, the borrower will owe me $4,560 - $700 ($100 per month for 7 months) = $3,860.
After February, he'll owe me $3,860 - $1,100 = $2,760.
As of the following January, he'll owe $2,760 - $1,100 ($100 per month for 11 months) = $1,660.
After that Febuary, he'll owe $1,660 - $1,100 = $560.
He'll be all paid off six months after that.
Adding it up, I get 7 months + 1 month + 11 months + 1 month + 6 months = 26 months.
I'm decent at using a spreadsheet, so here's how I set up the problem and solved it in Excel: