THE SCENARIO
John and Jane Smith want to retire in 12 years, they currently have $250,000 invested in a bond fund earning 2.8%, and they need $875,000 to retire.
THE QUESTION
Let's say that they arbitrarily decide that they need 18% on their money because they haven't actually done the calculations to know what they really need and a family member told them just must have 18%.
It takes them 2 years to find an 18% investment, and when they find one, it runs for a year and then ends (high-yield investments can be pretty short sometimes).
Previously, we did these calculations assuming the Smiths would not invest any additional money on a monthly basis. Now let's see what the numbers look like if they will invest an additional $250 per month.
A) How much money do they have after that investment ends?
Keep in mind that their current bond fund is paying them a 2.8% yield. Assume that they're not adding any additional money to the investment during this time period.
B) What yield do they need to get on that money in the 9 following years until they retire?
THE SOLUTION
A)How much money do they have after that investment ends?
We'll break this down into two TVM problems. First, we'll calculate how much their money grows in the bond fund while waiting for 2 years (24 months), then we'll calculate how much their money grows in the 18% return for 1 year (12 months).
N: 24
I/YR: 2.8%
PV: -$250,000
PMT: -$250
FV: $270,545.96
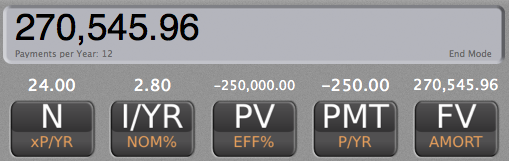
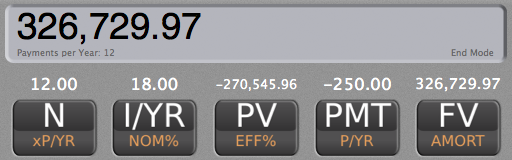
FV after the first two years becomes PV at the beginning of year 3.
N: 12
I/YR: 18%
PV: -$270,545.96
PMT: $250
FV: $326,729.97
At the end of the third year, they will have $326,729.97 in their investment account.
B)What yield do they need to get on that money in the 9 following years until they retire?
N = 108
PV = -$326,729.97
PMT = -$250
FV = $875,000
I/YR = 10.41%
So by waiting for 3 years, even though they managed to find a 18% investment for a year, they need to get an 10.41% return for the next 9 yearsin order to meet their retirement goals.
