See all of the Money Blog entries in this series.
THE SCENARIO
John and Jane Smith want to retire in 12 years, they currently have $250,000, and they need $875,000 to retire. If they invested their money at 2.8% for two years, and then at 18% for the next year, they would have $316,100.13 at the end of year 3.
THE QUESTION
If they'd immediately found a 10.5% investment at the beginning,
A) How much money would they have at the end of these same 3 years?
B) How much money would they have at the end of these same 3 years if they contributed and additional $250 per month?
THE SOLUTION
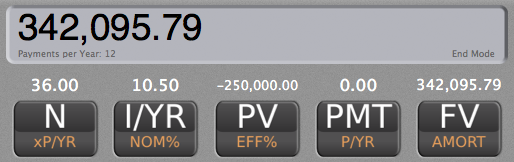
A)How much money would they have at the end of these same 3 years?
N = 36
I/YR = 10.5%
PV = -$250,000
PMT = $0
FV = $342,095.79
At the end of 3 years, they'd have $342,095.79.
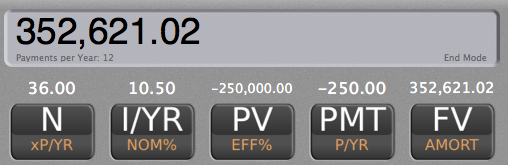
B)How much money would they have at the end of these same 3 years if they contributed and additional $250 per month?
N = 36
I/YR = 10.5%
PV = -$250,000
PMT = -$250
FV = $352,621.02
At the end of 3 years, they'd have $352,621.02.
DISCUSSION
Comparing #3 and #4 with this question, we note that by waiting for an 18% return, the Smiths actually end up with less money than if they'd invested at a 10.5% return right away. To summarize:
If they invested their $250,000 at 2.8% then 18%, they would end up with $316,100.13.
If they invested their $250,000 at 10.5% right away, they would end up with $342,095.79.
If they invested their $250,000, plus an additional $250 per month, at 2.8% then 18%, they would end up with $326,729.97.
If they invested their $250,000, plus an additional $250 per month, at 10.5% right away, they would end up with $352,621.02.
Why is this?The simple answer is "time". That is, by keeping their investment earning a relatively low 2.8% for two years, they have so much ground to make up (in comparison with the 10.5% return scenario) that a year of 18% is unable to compensate fully. If they could get 18% for more time, eventually the 'wait then invest at a high rate' would eventually catch up to the '10.5% from the beginning' scenario... but high-yield returns can be short-lived, and are harder to come by than more modest-yield investments.
Using a bit of trial and error, it becomes apparent that if the Smiths can get 18% on their money for a bit longer than 2 years (just over 24 months), they will make more money than if they get 10.5% over the same period of time.