Okay, time for part 3. To recap, the scenario from Part 1 and Part 2 is as follows:
THE SCENARIO
I came across a note for sale. The terms of the note are as follows:
Original balance: $6,000
Unpaid balance as of June 2: $4,560
Term: 5 years
Interest Rate: 0
Payments: $100 per month
If I buy it, make the purchase on June 2, and the first payment I'll receive will be the July payment.
Every February, the borrower pays off $1,000 in order to accelerate the note paydown.
QUESTION
The current owner of the note wants to sell me the note for 15% off its face value (85% of $4,560 = $3,876).
If I buy, what will my yield be if the borrower pays normally but without his extra lump-sum payment every February?
SOLUTION
I can do this with normal a Time Value of Money calculation.
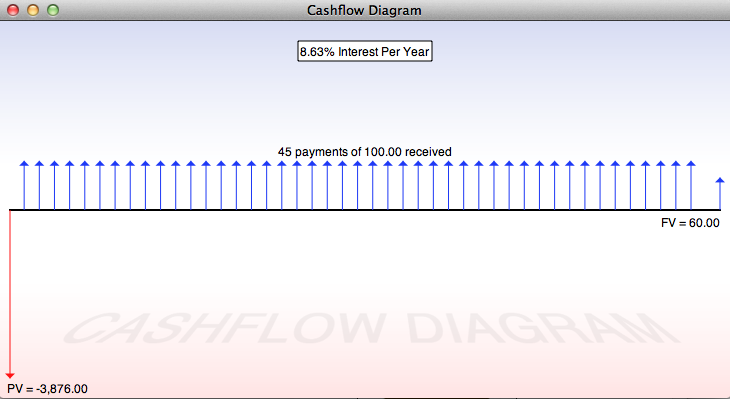
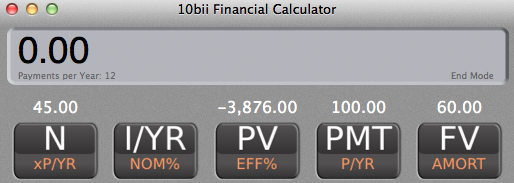
N is 45 ($4,560 divided by $100, rounding down).
PV is -$3,876
PMT is $100
FV is $60
Here's the problem setup:
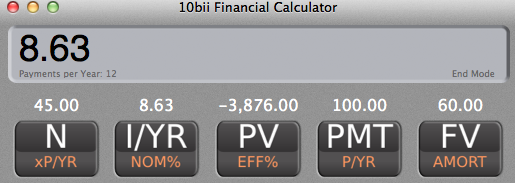
Solving for I/YR, I find that my yield is 8.63%.
Here's what the cashflow diagram looks like: